IMO Shortlist 2013 problem G2
Kvaliteta:
Avg: 3,0Težina:
Avg: 6,0 Let  be the circumcircle of a triangle
be the circumcircle of a triangle  . Denote by
. Denote by  and
and  the midpoints of the sides
the midpoints of the sides  and
and  , respectively, and denote by
, respectively, and denote by  the midpoint of the arc
the midpoint of the arc  of
of  not containing
not containing  . The circumcircles of the triangles
. The circumcircles of the triangles 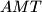 and
and 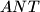 intersect the perpendicular bisectors of
intersect the perpendicular bisectors of  and
and  at points
at points  and
and  , respectively; assume that
, respectively; assume that  and
and  lie inside the triangle
lie inside the triangle  . The lines
. The lines  and
and  intersect at
intersect at  . Prove that
. Prove that 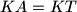 .
.
 be the circumcircle of a triangle
be the circumcircle of a triangle  . Denote by
. Denote by  and
and  the midpoints of the sides
the midpoints of the sides  and
and  , respectively, and denote by
, respectively, and denote by  the midpoint of the arc
the midpoint of the arc  of
of  not containing
not containing  . The circumcircles of the triangles
. The circumcircles of the triangles 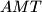 and
and 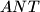 intersect the perpendicular bisectors of
intersect the perpendicular bisectors of  and
and  at points
at points  and
and  , respectively; assume that
, respectively; assume that  and
and  lie inside the triangle
lie inside the triangle  . The lines
. The lines  and
and  intersect at
intersect at  . Prove that
. Prove that 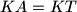 .
. Izvor: Iran
 Školjka
Školjka 
