Let

be a triangle with
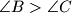
. Let

and

be two different points on line

such that
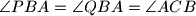
and

is located between

and

. Suppose that there exists and interior point

of segment
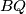
for which
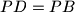
. Let the ray

intersect the circle

at
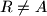
. Prove that
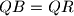
.
%V0
Let $ABC$ be a triangle with $\angle B > \angle C$. Let $P$ and $Q$ be two different points on line $AC$ such that $\angle PBA = \angle QBA = \angle ACB$ and $A$ is located between $P$ and $C$. Suppose that there exists and interior point $D$ of segment $BQ$ for which $PD = PB$. Let the ray $AD$ intersect the circle $ABC$ at $R \neq A$. Prove that $QB = QR$.