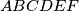
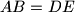
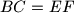
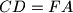
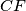
Let be a convex hexagon with , , , and . Prove that the diagonals , , and are concurrent.
%V0
Let $ABCDEF$ be a convex hexagon with $AB = DE$, $BC = EF$, $CD = FA$, and $\angle A - \angle D = \angle C - \angle F = \angle E - \angle B$. Prove that the diagonals $AD$, $BE$, and $CF$ are concurrent.
Školjka 
be a convex hexagon with 
, 
, 
, and 
. Prove that the diagonals 
, 
, and 
are concurrent.