Determine whether there exists an infinite sequence of nonzero digits
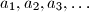
and a positive integer

such that for every integer
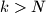
, the number
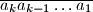
is a perfect square.
%V0
Determine whether there exists an infinite sequence of nonzero digits $a_1, a_2, a_3, \ldots$ and a positive integer $N$ such that for every integer $k > N$, the number $\overline{a_k a_{k-1} \ldots a_1}$ is a perfect square.