IMO Shortlist 2013 problem N5
Kvaliteta:
Avg: 3,0Težina:
Avg: 8,0 Fix an integer 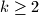 . Two players, called Ana and Banana, play the following game of numbers. Initially, some integer
. Two players, called Ana and Banana, play the following game of numbers. Initially, some integer 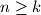 gets written on the blackboard. Then they make moves in turn, with Ana beginning. A player making a move erases the number
gets written on the blackboard. Then they make moves in turn, with Ana beginning. A player making a move erases the number  just written on the blackboard and replaced it by some number
just written on the blackboard and replaced it by some number 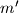 with
with 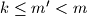 that is coprime to
that is coprime to  . The first player who cannot move anymore loses.
. The first player who cannot move anymore loses.
An integer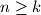 is called good if Banana has a winning strategy when the initial number is
is called good if Banana has a winning strategy when the initial number is  , and bad otherwise.
, and bad otherwise.
Consider two integers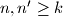 with the property that each prime number
with the property that each prime number 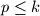 divides
divides  if and only if it divides
if and only if it divides 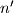 . Prove that either both
. Prove that either both  and
and 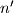 are good or both are bad.
are good or both are bad.
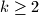 . Two players, called Ana and Banana, play the following game of numbers. Initially, some integer
. Two players, called Ana and Banana, play the following game of numbers. Initially, some integer 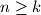 gets written on the blackboard. Then they make moves in turn, with Ana beginning. A player making a move erases the number
gets written on the blackboard. Then they make moves in turn, with Ana beginning. A player making a move erases the number  just written on the blackboard and replaced it by some number
just written on the blackboard and replaced it by some number 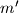 with
with 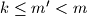 that is coprime to
that is coprime to  . The first player who cannot move anymore loses.
. The first player who cannot move anymore loses.An integer
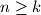 is called good if Banana has a winning strategy when the initial number is
is called good if Banana has a winning strategy when the initial number is  , and bad otherwise.
, and bad otherwise.Consider two integers
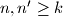 with the property that each prime number
with the property that each prime number 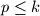 divides
divides  if and only if it divides
if and only if it divides 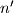 . Prove that either both
. Prove that either both  and
and 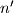 are good or both are bad.
are good or both are bad. Izvor: Italy
 Školjka
Školjka 
