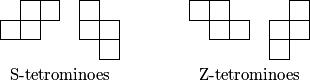
Construct a tetromino by attaching 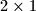 dominoes along their longer sides such that the midpoint of the longer side of one domino is a corner of the other domino. This construction yields two kinds of tetrominoes with opposite orientations. Let us call them S- and Z-tetrominoes, respectively.
dominoes along their longer sides such that the midpoint of the longer side of one domino is a corner of the other domino. This construction yields two kinds of tetrominoes with opposite orientations. Let us call them S- and Z-tetrominoes, respectively.
Assume that a lattice polygon  can be tiled with S-tetrominoes. Prove that no matter how we tile
can be tiled with S-tetrominoes. Prove that no matter how we tile  using only S- and Z-tetrominoes, we always use an even number of Z-tetrominoes.
using only S- and Z-tetrominoes, we always use an even number of Z-tetrominoes.
Construct a tetromino by attaching $2 \times 1$ dominoes along their longer sides such that the midpoint of the longer side of one domino is a corner of the other domino. This construction yields two kinds of tetrominoes with opposite orientations. Let us call them S- and Z-tetrominoes, respectively.
% $$
% \begin{tikzpicture}[scale=.4]
% \filldraw[fill=lightgray] (0, 1) -- (2, 1) -- (2, 2) -- (3, 2) -- (3, 3) -- (1, 3) -- (1, 2) -- (0, 2) -- cycle;
% \draw (1, 1) -- (1, 2) -- (2, 2) -- (2, 3);
% \filldraw[fill=lightgray] (4, 1) -- (5, 1) -- (5, 0) -- (6, 0) -- (6, 2) -- (5, 2) -- (5, 3) -- (4, 3) -- cycle;
% \draw (6, 1) -- (5, 1) -- (5, 2) -- (4, 2);
% \node[below] at (3, 0) {S-tetrominoes};
% \end{tikzpicture}
% \quad\quad\quad\quad
% \begin{tikzpicture}[scale=.4]
% \filldraw[fill=lightgray] (1, 1) -- (3, 1) -- (3, 2) -- (2, 2) -- (2, 3) -- (0, 3) -- (0, 2) -- (1, 2) -- cycle;
% \draw (2, 1) -- (2, 2) -- (1, 2) -- (1, 3);
% \filldraw[fill=lightgray] (4, 0) -- (5, 0) -- (5, 1) -- (6, 1) -- (6, 3) -- (5, 3) -- (5, 2) -- (4, 2) -- cycle;
% \draw (4, 1) -- (5, 1) -- (5, 2) -- (6, 2);
% \node[below] at (3, 0) {Z-tetrominoes};
% \end{tikzpicture}
% $$
$$
\setlength{\unitlength}{12pt}
\begin{picture}(7, 4)
\put(0, 2){\line(1, 0){2}}
\put(0, 3){\line(1, 0){3}}
\put(1, 4){\line(1, 0){2}}
\put(0, 2){\line(0, 1){1}}
\put(1, 2){\line(0, 1){2}}
\put(2, 2){\line(0, 1){2}}
\put(3, 3){\line(0, 1){1}}
%
\put(5, 1){\line(1, 0){1}}
\put(4, 2){\line(1, 0){2}}
\put(4, 3){\line(1, 0){2}}
\put(4, 4){\line(1, 0){1}}
\put(4, 2){\line(0, 1){2}}
\put(5, 1){\line(0, 1){3}}
\put(6, 1){\line(0, 1){2}}
\put(.5, 0){\text{S-tetrominoes}}
\end{picture}
%
\quad\quad\quad
\begin{picture}(7, 4)
\put(1, 2){\line(1, 0){2}}
\put(0, 3){\line(1, 0){3}}
\put(0, 4){\line(1, 0){2}}
\put(0, 3){\line(0, 1){1}}
\put(1, 2){\line(0, 1){2}}
\put(2, 2){\line(0, 1){2}}
\put(3, 2){\line(0, 1){1}}
%
\put(4, 1){\line(1, 0){1}}
\put(4, 2){\line(1, 0){2}}
\put(4, 3){\line(1, 0){2}}
\put(5, 4){\line(1, 0){1}}
\put(4, 1){\line(0, 1){2}}
\put(5, 1){\line(0, 1){3}}
\put(6, 2){\line(0, 1){2}}
\put(.5, 0){\text{Z-tetrominoes}}
\end{picture}
$$
Assume that a lattice polygon $P$ can be tiled with S-tetrominoes. Prove that no matter how we tile $P$ using only S- and Z-tetrominoes, we always use an even number of Z-tetrominoes.
\begin{flushright}\emph{(Hungary)}\end{flushright}
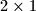 dominoes along their longer sides such that the midpoint of the longer side of one domino is a corner of the other domino. This construction yields two kinds of tetrominoes with opposite orientations. Let us call them S- and Z-tetrominoes, respectively.
dominoes along their longer sides such that the midpoint of the longer side of one domino is a corner of the other domino. This construction yields two kinds of tetrominoes with opposite orientations. Let us call them S- and Z-tetrominoes, respectively.
 can be tiled with S-tetrominoes. Prove that no matter how we tile
can be tiled with S-tetrominoes. Prove that no matter how we tile  using only S- and Z-tetrominoes, we always use an even number of Z-tetrominoes.
using only S- and Z-tetrominoes, we always use an even number of Z-tetrominoes. Školjka
Školjka 
