Školjka

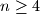Let $M$ be a set of $n \geq 4$ points in the plane, no three of which are collienar. Initially these points are connected with $n$ segments so that each point in $M$ is the endpoint of exactly two segments. Then, at each step, one may choose two segments $AB$ and $CD$ sharing a common interior point and replace them by the segments $AC$ and $BD$ if none of them is present at this moment. 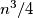Prove that it is impossible to perform $n^3 / 4$ or more such moves. \begin{flushright}\emph{(Russia)}\end{flushright}