Let be a triangle. The points , , and lie on the segments , , and , respectively, such that the lines 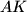, , 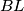and 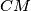intersect in a common point. Prove that it is possible to choose two of the triangles 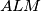, , 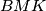and 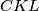whose inradii sum up to at least the inradius of the triangle .
(Estonia)
Let $ABC$ be a triangle. The points $K$, $L$, and $M$ lie on the segments $BC$, $CA$, and $AB$, respectively, such that the lines $AK$, $BL$, and $CM$ intersect in a common point. Prove that it is possible to choose two of the triangles $ALM$, $BMK$, and $CKL$ whose inradii sum up to at least the inradius of the triangle $ABC$.
\begin{flushright}\emph{(Estonia)}\end{flushright}
Školjka 
be a triangle. The points 
, 
, and 
lie on the segments 
, 
, and 
, respectively, such that the lines 
, 
, and 
intersect in a common point. Prove that it is possible to choose two of the triangles 
, 
, and 
whose inradii sum up to at least the inradius of the triangle