IMO Shortlist 2014 problem G4
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0Consider a fixed circle  with three fixed points
with three fixed points  ,
,  and
and  on it. Also, let us fix a real number
on it. Also, let us fix a real number 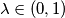 . For a variable points
. For a variable points 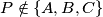 on
on  , let
, let  be the point on the segment
be the point on the segment 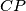 such that
such that 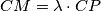 . Let
. Let  be the second point of intersection of the circumcircles of the triangles
be the second point of intersection of the circumcircles of the triangles 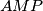 and
and 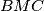 . Prove that as
. Prove that as  varies, the point
varies, the point  lies on a fixed circle.
lies on a fixed circle.
(United Kingdom)
Izvor: https://www.imo-official.org/problems/IMO2014SL.pdf
 Školjka
Školjka 
