Školjka

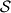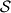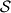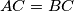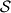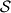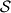We say that a finite set $\mathcal{S}$ of points in the plane is \emph{balanced} if, for any two different points $A$ and $B$ in $\mathcal{S}$, there is a point $C$ in $\mathcal{S}$ such that $AC=BC$. We say that $\mathcal{S}$ is \emph{centre-free} if for any three different points $A$, $B$ and $C$ in $\mathcal{S}$, there is no points $P$ in $\mathcal{S}$ such that 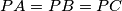$PA=PB=PC$. \\(a) Show that for all integers 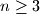$n\ge 3$, there exists a balanced set consisting of $n$ points. \\\\ (b) Determine all integers 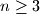$n\ge 3$ for which there exists a balanced centre-free set consisting of $n$ points. \\ \begin{flushright}\emph{(Netherlands)}\end{flushright}