IMO Shortlist 2015 problem G2
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0Triangle  has circumcircle
has circumcircle  and circumcenter
and circumcenter  . A circle
. A circle  with center
with center  intersects the segment
intersects the segment  at points
at points  and
and  , such that
, such that  ,
,  ,
,  , and
, and  are all different and lie on line
are all different and lie on line  in this order. Let
in this order. Let  and
and  be the points of intersection of
be the points of intersection of  and
and  , such that
, such that  ,
,  ,
,  ,
,  , and
, and  lie on
lie on  in this order. Let
in this order. Let  be the second point of intersection of the circumcircle of triangle
be the second point of intersection of the circumcircle of triangle 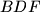 and the segment
and the segment  . Let
. Let  be the second point of intersection of the circumcircle of triangle
be the second point of intersection of the circumcircle of triangle 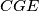 and the segment
and the segment  .
.
Suppose that the lines 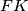 and
and 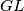 are different and intersect at the point
are different and intersect at the point  . Prove that
. Prove that  lies on the line
lies on the line 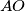 .
.
(Greece)
Izvor: https://www.imo-official.org/problems/IMO2015SL.pdf
 Školjka
Školjka 
