IMO Shortlist 2015 problem G6
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0Let  be an acute triangle with
be an acute triangle with  . Let
. Let  be its cirumcircle,
be its cirumcircle,  its orthocenter, and
its orthocenter, and  the foot of the altitude from
the foot of the altitude from  . Let
. Let  be the midpoint of
be the midpoint of  . Let
. Let  be the point on
be the point on  such that
such that 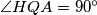 and let
and let  be the point on
be the point on  such that
such that 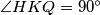 . Assume that the points
. Assume that the points  ,
,  ,
,  ,
,  and
and  are all different and lie on
are all different and lie on  in this order.
in this order.
Prove that the circumcircles of triangles 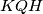 and
and 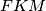 are tangent to each other.
are tangent to each other.
(Ukraine)
Izvor: https://www.imo-official.org/problems/IMO2015SL.pdf
 Školjka
Školjka 
