Find all positive integers  such that the following statement holds: Suppose real numbers
such that the following statement holds: Suppose real numbers  ,
,  ,
,  ,
,  ,
, 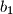 ,
, 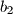 ,
,  ,
, 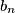 satisfy
satisfy 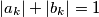 for all
for all 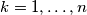 . Then there exists
. Then there exists 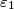 ,
, 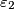 ,
,  ,
, 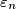 , each of which is either
, each of which is either  or
or  , such that
, such that 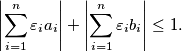
Find all positive integers $n$ such that the following statement holds: Suppose real numbers $a_1$, $a_2$, $\dots$, $a_n$, $b_1$, $b_2$, $\dots$, $b_n$ satisfy $|a_k|+|b_k|=1$ for all $k=1,\dots,n$. Then there exists $\varepsilon_1$, $\varepsilon_2$, $\dots$, $\varepsilon_n$, each of which is either $-1$ or $1$, such that
\[ \left| \sum_{i=1}^n \varepsilon_i a_i \right| + \left| \sum_{i=1}^n \varepsilon_i b_i \right| \le 1. \]