Školjka

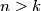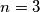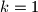The leader of an IMO team chooses positive integers $n$ and $k$ with $n > k$, and announces them to the deputy leader and a contestant. The leader then secretly tells the deputy leader an $n$-digit binary string, and the deputy leader writes down all $n$-digit binary strings which differ from the leader’s in exactly $k$ positions. 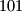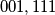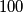(For example, if $n = 3$ and $k = 1$, and if the leader chooses $101$, the deputy leader would write down $001, 111$ and $100$.) The contestant is allowed to look at the strings written by the deputy leader and guess the leader’s string. What is the minimum number of guesses (in terms of $n$ and $k$) needed to guarantee the correct answer?