IMO Shortlist 2016 problem C4
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0Find all integers  for which each cell of
for which each cell of 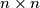 table can be filled with one of the letters
table can be filled with one of the letters 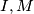 and
and  in such a way that: in each row and each column, one third of the entries are
in such a way that: in each row and each column, one third of the entries are  , one third are
, one third are  and one third are
and one third are  ; and in any diagonal, if the number of entries on the diagonal is a multiple of three, then one third of the entries are
; and in any diagonal, if the number of entries on the diagonal is a multiple of three, then one third of the entries are  , one third are
, one third are  and one third are
and one third are  . Note. The rows and columns of an
. Note. The rows and columns of an 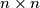 table are each labelled
table are each labelled  to
to  in a natural order. Thus each cell corresponds to a pair of positive integer
in a natural order. Thus each cell corresponds to a pair of positive integer 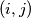 with
with 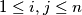 . For
. For 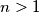 , the table has
, the table has 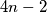 diagonals of two types. A diagonal of first type consists all cells
diagonals of two types. A diagonal of first type consists all cells 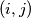 for which
for which 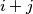 is a constant, and the diagonal of this second type consists all cells
is a constant, and the diagonal of this second type consists all cells 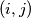 for which
for which 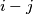 is constant.
is constant.
Izvor: https://www.imo-official.org/problems/IMO2016SL.pdf
 Školjka
Školjka 
