Let be a triangle with circumcircle and incenter and let be the midpoint of . The points , , are selected on sides , , such that , , and . Suppose that the circumcircle of intersects at a point other than . Prove that lines and meet on .
Let $ABC$ be a triangle with circumcircle $\Gamma$ and incenter $I$ and let $M$ be the midpoint of $\overline{BC}$. The points $D$, $E$, $F$ are selected on sides $\overline{BC}$, $\overline{CA}$, $\overline{AB}$ such that $\overline{ID} \perp \overline{BC}$, $\overline{IE}\perp \overline{AI}$, and $\overline{IF}\perp \overline{AI}$. Suppose that the circumcircle of $\triangle AEF$ intersects $\Gamma$ at a point $X$ other than $A$. Prove that lines $XD$ and $AM$ meet on $\Gamma$.
Cini se da se jedino moze length bashem rijesiti. :(
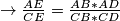tetivan, presjek dijagonala (preko sinusa ili povrsina) je potrebna lemma.
zapravo ak samo razmisljas o omjerima moze se rijesit u 2min
Cini se da se jedino moze length bashem rijesiti. :(
$ABCD$ tetivan, $E$ presjek dijagonala $\rightarrow \frac{AE}{CE}=\frac{AB*AD}{CB*CD}$ (preko sinusa ili povrsina) je potrebna lemma.
zapravo ak samo razmisljas o omjerima moze se rijesit u 2min
Školjka 
be a triangle with circumcircle 
and incenter 
and let 
be the midpoint of 
. The points 
, 
, 
are selected on sides 
, 
such that 
, 
, and 
. Suppose that the circumcircle of 
intersects 
other than 
. Prove that lines 
and 
meet on 
tetivan, 
(preko sinusa ili povrsina) je potrebna lemma.