IMO Shortlist 2016 problem G3
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0Let 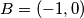 and
and 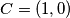 be fixed points on the coordinate plane. A nonempty, bounded subset
be fixed points on the coordinate plane. A nonempty, bounded subset  of the plane is said to be nice if
of the plane is said to be nice if
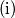 there is a point
there is a point  in
in  such that for every point
such that for every point  in
in  , the segment
, the segment 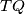 lies entirely in
lies entirely in  ; and
; and
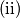 for any triangle
for any triangle 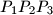 , there exists a unique point
, there exists a unique point  in
in  and a permutation
and a permutation 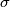 of the indices
of the indices 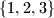 for which triangles
for which triangles  and
and 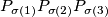 are similar.
are similar.
Prove that there exist two distinct nice subsets  and
and  of the set
of the set 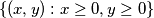 such that if
such that if 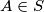 and
and 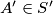 are the unique choices of points in
are the unique choices of points in 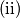 , then the product
, then the product 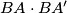 is a constant independent of the triangle
is a constant independent of the triangle 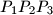 .
.
Izvor: https://www.imo-official.org/problems/IMO2016SL.pdf
 Školjka
Školjka 
