IMO Shortlist 2016 problem N3
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0A set of postive integers is called fragrant if it contains at least two elements and each of its elements has a prime factor in common with at least one of the other elements. Let 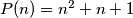 . What is the least possible positive integer value of
. What is the least possible positive integer value of  such that there exists a non-negative integer
such that there exists a non-negative integer  for which the set
for which the set 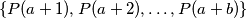 is fragrant?
is fragrant?
Izvor: https://www.imo-official.org/problems/IMO2016SL.pdf
 Školjka
Školjka 
