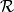A rectangle with odd integer side lengths is divided into small rectangles with integer side lengths. Prove that there is at least one among the small rectangles whose distances from the four sides of 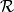are either all odd or all even.
A rectangle $\mathcal{R}$ with odd integer side lengths is divided into small rectangles with integer side lengths.
Prove that there is at least one among the small rectangles whose distances from the four sides of $\mathcal{R}$ are either all odd or all even.
Školjka 
with odd integer side lengths is divided into small rectangles with integer side lengths. Prove that there is at least one among the small rectangles whose distances from the four sides of