IMO Shortlist 2017 problem C3
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0Sir Alex plays the following game on a row of 9 cells. Initially, all cells are empty. In each move, Sir Alex is allowed to perform exactly one of the following two operations:
(1) Choose any number of the form 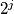 , where
, where  is a non-negative integer, and put it into an empty cell.
is a non-negative integer, and put it into an empty cell.
(2) Choose two (not necessarily adjacent) cells with the same number in them; denote that number by 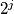 . Replace the number in one of the cells with
. Replace the number in one of the cells with 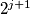 and erase the number in the other cell.
and erase the number in the other cell.
At the end of the game, one cell contains 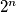 , where
, where  is a given positive integer, while the other cells are empty. Determine the maximum number of moves that Sir Alex could have made, in terms of
is a given positive integer, while the other cells are empty. Determine the maximum number of moves that Sir Alex could have made, in terms of  .
.
Izvor: https://www.imo-official.org/problems/IMO2017SL.pdf
 Školjka
Školjka 
