Školjka

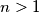Let $n > 1$ be a given integer. An 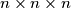$n \times n \times n$ cube is composed of 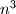$n^3$ unit cubes. Each unit cube is painted with one colour. For each 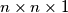$n \times n \times 1$ box consisting of 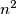$n^2$ unit cubes (in any of the three possible orientations), we consider the set of colours present in that box (each colour is listed only once). This way, we get 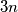$3n$ sets of colours, split into three groups according to the orientation. It happens that for every set in any group, the same set appears in both of the other groups. Determine, in terms of $n$, the maximal possible number of colours that are present.