IMO Shortlist 2017 problem G2
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0Let  and
and  be different points on a circle
be different points on a circle  such that
such that 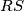 is not a diameter. Let
is not a diameter. Let 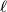 be the tangent line to
be the tangent line to  at
at  . Point
. Point  is such that
is such that  is the midpoint of the line segment
is the midpoint of the line segment 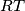 . Point
. Point 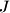 is chosen on the shorter arc
is chosen on the shorter arc 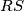 of
of  so that the circumcircle
so that the circumcircle  of triangle
of triangle 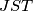 intersects
intersects 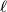 at two distinct points. Let
at two distinct points. Let  be the common point of
be the common point of  and
and 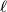 that is closer to
that is closer to  . Line
. Line 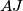 meets
meets  again at
again at  . Prove that the line
. Prove that the line 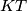 is tangent to
is tangent to  .
.
Izvor: https://www.imo-official.org/problems/IMO2017SL.pdf
 Školjka
Školjka 
