IMO Shortlist 2017 problem N4
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0Call a rational number short if it has finitely many digits in its decimal expansion. For a positive integer  , we say that a positive integer
, we say that a positive integer  is
is  tastic if there exists a number
tastic if there exists a number 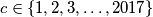 such that
such that 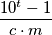 is short, and such that
is short, and such that 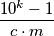 is not short for any
is not short for any 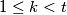 . Let
. Let 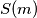 be the the set of
be the the set of  tastic numbers. Consider
tastic numbers. Consider 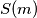 for
for 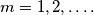 What is the maximum number of elements in
What is the maximum number of elements in 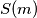 ?
?
Izvor: https://www.imo-official.org/problems/IMO2017SL.pdf
 Školjka
Školjka 
