IMO Shortlist 2018 problem C3
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0Let  be a given positive integer. Sisyphus performs a sequence of turns on a board consisting of
be a given positive integer. Sisyphus performs a sequence of turns on a board consisting of  squares in a row, numbered
squares in a row, numbered  to
to  from left to right. Initially,
from left to right. Initially,  stones are put into square
stones are put into square  , and the other squares are empty. At every turn, Sisyphus chooses any nonempty square, say with
, and the other squares are empty. At every turn, Sisyphus chooses any nonempty square, say with  stones, takes one of these stones and moves it to the right by at most
stones, takes one of these stones and moves it to the right by at most  squares (the stone should say within the board). Sisyphus' aim is to move all
squares (the stone should say within the board). Sisyphus' aim is to move all  stones to square
stones to square  . Prove that Sisyphus cannot reach the aim in less than
. Prove that Sisyphus cannot reach the aim in less than 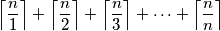 turns. (As usual,
turns. (As usual, 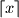 stands for the least integer not smaller than
stands for the least integer not smaller than  . )
. )
Izvor: https://www.imo-official.org/problems/IMO2018SL.pdf
 Školjka
Školjka 
