A point  is chosen inside a triangle
is chosen inside a triangle  . Let
. Let  ,
,  , and
, and  be the reflections of
be the reflections of  in
in  ,
,  , and
, and  , respectively. Let
, respectively. Let  be the circumcircle of the triangle
be the circumcircle of the triangle 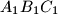 . The lines
. The lines 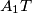 ,
, 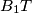 , and
, and 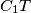 meet
meet  again at
again at  ,
,  , and
, and 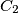 , respectively. Prove that the lines
, respectively. Prove that the lines 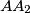 ,
, 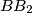 , and
, and 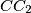 are concurrent on
are concurrent on  .
.
A point $T$ is chosen inside a triangle $ABC$. Let $A_1$, $B_1$, and $C_1$ be the reflections of $T$ in $BC$, $CA$, and $AB$, respectively. Let $\Omega$ be the circumcircle of the triangle $A_1B_1C_1$. The lines $A_1T$, $B_1T$, and $C_1T$ meet $\Omega$ again at $A_2$, $B_2$, and $C_2$, respectively. Prove that the lines $AA_2$, $BB_2$, and $CC_2$ are concurrent on $\Omega$.