Školjka

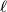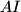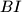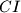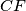Let $ABC$ be a triangle with circumcircle $\omega$ and incentre $I$. A line $\ell$ intersects the lines $AI$, $BI$, and $CI$ at points $D$, $E$, and $F$, respectively, distinct from the points $A$, $B$, $C$, and $I$. The perpendicular bisectors $x$, $y$, and $z$ of the segments $AD$, $BE$, and $CF$, respectively determine a triangle 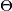$\Theta$. Show that the circumcircle of the triangle 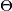$\Theta$ is tangent to $\Omega$.