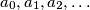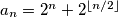Define the sequence by . Prove that there are infinitely many terms of the sequence which can be expressed as a sum of (two or more) distinct terms of the sequence, as well as infinitely many of those which cannot be expressed in such a way.
Define the sequence $a_0,a_1,a_2,\hdots$ by $a_n=2^n+2^{\lfloor n/2\rfloor}$. Prove that there are infinitely many terms of the sequence which can be expressed as a sum of (two or more) distinct terms of the sequence, as well as infinitely many of those which cannot be expressed in such a way.
Školjka 
by 
. Prove that there are infinitely many terms of the sequence which can be expressed as a sum of (two or more) distinct terms of the sequence, as well as infinitely many of those which cannot be expressed in such a way.