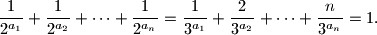The liar's guessing game is a game played between two players  and
and  . The rules of the game depend on two positive integers
. The rules of the game depend on two positive integers  and
and  which are known to both players.
which are known to both players.
At the start of the game chooses integers
chooses integers  and
and  with
with 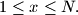 Player
Player  keeps
keeps  secret, and truthfully tells
secret, and truthfully tells  to player
to player  . Player
. Player  now tries to obtain information about
now tries to obtain information about  by asking player
by asking player  questions as follows: each question consists of
questions as follows: each question consists of  specifying an arbitrary set
specifying an arbitrary set  of positive integers (possibly one specified in some previous question), and asking
of positive integers (possibly one specified in some previous question), and asking  whether
whether  belongs to
belongs to  . Player
. Player  may ask as many questions as he wishes. After each question, player
may ask as many questions as he wishes. After each question, player  must immediately answer it with yes or no, but is allowed to lie as many times as she wants; the only restriction is that, among any
must immediately answer it with yes or no, but is allowed to lie as many times as she wants; the only restriction is that, among any 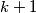 consecutive answers, at least one answer must be truthful.
consecutive answers, at least one answer must be truthful.
After has asked as many questions as he wants, he must specify a set
has asked as many questions as he wants, he must specify a set  of at most
of at most  positive integers. If
positive integers. If  belongs to
belongs to  , then
, then  wins; otherwise, he loses. Prove that:
wins; otherwise, he loses. Prove that:
1. If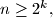 then
then  can guarantee a win.
can guarantee a win.
2. For all sufficiently large , there exists an integer
, there exists an integer 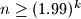 such that
such that  cannot guarantee a win.
cannot guarantee a win.
Proposed by David Arthur, Canada
 and
and  . The rules of the game depend on two positive integers
. The rules of the game depend on two positive integers  and
and  which are known to both players.
which are known to both players.At the start of the game
 chooses integers
chooses integers  and
and  with
with 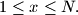 Player
Player  keeps
keeps  secret, and truthfully tells
secret, and truthfully tells  to player
to player  . Player
. Player  now tries to obtain information about
now tries to obtain information about  by asking player
by asking player  questions as follows: each question consists of
questions as follows: each question consists of  specifying an arbitrary set
specifying an arbitrary set  of positive integers (possibly one specified in some previous question), and asking
of positive integers (possibly one specified in some previous question), and asking  whether
whether  belongs to
belongs to  . Player
. Player  may ask as many questions as he wishes. After each question, player
may ask as many questions as he wishes. After each question, player  must immediately answer it with yes or no, but is allowed to lie as many times as she wants; the only restriction is that, among any
must immediately answer it with yes or no, but is allowed to lie as many times as she wants; the only restriction is that, among any 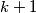 consecutive answers, at least one answer must be truthful.
consecutive answers, at least one answer must be truthful.After
 has asked as many questions as he wants, he must specify a set
has asked as many questions as he wants, he must specify a set  of at most
of at most  positive integers. If
positive integers. If  belongs to
belongs to  , then
, then  wins; otherwise, he loses. Prove that:
wins; otherwise, he loses. Prove that:1. If
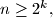 then
then  can guarantee a win.
can guarantee a win.2. For all sufficiently large
 , there exists an integer
, there exists an integer 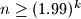 such that
such that  cannot guarantee a win.
cannot guarantee a win.Proposed by David Arthur, Canada
Given triangle  the point
the point 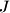 is the centre of the excircle opposite the vertex
is the centre of the excircle opposite the vertex 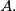 This excircle is tangent to the side
This excircle is tangent to the side  at
at  , and to the lines
, and to the lines  and
and  at
at  and
and  , respectively. The lines
, respectively. The lines 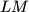 and
and 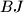 meet at
meet at  , and the lines
, and the lines 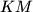 and
and 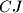 meet at
meet at 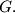 Let
Let  be the point of intersection of the lines
be the point of intersection of the lines 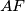 and
and  , and let
, and let  be the point of intersection of the lines
be the point of intersection of the lines 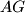 and
and 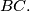 Prove that
Prove that  is the midpoint of
is the midpoint of 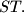
(The excircle of opposite the vertex
opposite the vertex  is the circle that is tangent to the line segment
is the circle that is tangent to the line segment  , to the ray
, to the ray  beyond
beyond  , and to the ray
, and to the ray  beyond
beyond  .)
.)
Proposed by Evangelos Psychas, Greece
 the point
the point 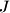 is the centre of the excircle opposite the vertex
is the centre of the excircle opposite the vertex 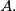 This excircle is tangent to the side
This excircle is tangent to the side  at
at  , and to the lines
, and to the lines  and
and  at
at  and
and  , respectively. The lines
, respectively. The lines 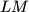 and
and 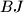 meet at
meet at  , and the lines
, and the lines 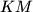 and
and 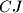 meet at
meet at 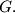 Let
Let  be the point of intersection of the lines
be the point of intersection of the lines 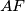 and
and  , and let
, and let  be the point of intersection of the lines
be the point of intersection of the lines 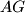 and
and 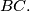 Prove that
Prove that  is the midpoint of
is the midpoint of 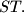
(The excircle of
 opposite the vertex
opposite the vertex  is the circle that is tangent to the line segment
is the circle that is tangent to the line segment  , to the ray
, to the ray  beyond
beyond  , and to the ray
, and to the ray  beyond
beyond  .)
.)Proposed by Evangelos Psychas, Greece
Let  be a triangle with
be a triangle with 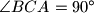 , and let
, and let  be the foot of the altitude from
be the foot of the altitude from  . Let
. Let  be a point in the interior of the segment
be a point in the interior of the segment  . Let
. Let  be the point on the segment
be the point on the segment 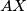 such that
such that 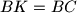 . Similarly, let
. Similarly, let  be the point on the segment
be the point on the segment 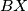 such that
such that 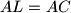 . Let
. Let  be the point of intersection of
be the point of intersection of 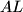 and
and 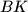 .
.
Show that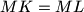 .
.
Proposed by Josef Tkadlec, Czech Republic
 be a triangle with
be a triangle with 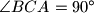 , and let
, and let  be the foot of the altitude from
be the foot of the altitude from  . Let
. Let  be a point in the interior of the segment
be a point in the interior of the segment  . Let
. Let  be the point on the segment
be the point on the segment 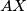 such that
such that 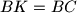 . Similarly, let
. Similarly, let  be the point on the segment
be the point on the segment 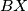 such that
such that 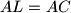 . Let
. Let  be the point of intersection of
be the point of intersection of 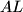 and
and 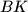 .
.Show that
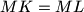 .
.Proposed by Josef Tkadlec, Czech Republic
 Školjka
Školjka 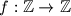 such that, for all integers
such that, for all integers  that satisfy
that satisfy 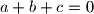 , the following equality holds:
, the following equality holds: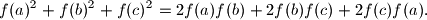
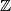 denotes the set of integers.)
denotes the set of integers.)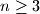 be an integer, and let
be an integer, and let 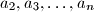 be positive real numbers such that
be positive real numbers such that 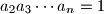 . Prove that
. Prove that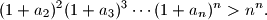
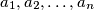 such that
such that