IMO Shortlist 2012 problem G1
Kvaliteta:
Avg: 0,0Težina:
Avg: 5,7 Given triangle  the point
the point 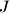 is the centre of the excircle opposite the vertex
is the centre of the excircle opposite the vertex 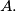 This excircle is tangent to the side
This excircle is tangent to the side  at
at  , and to the lines
, and to the lines  and
and  at
at  and
and  , respectively. The lines
, respectively. The lines 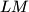 and
and 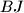 meet at
meet at  , and the lines
, and the lines 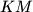 and
and 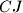 meet at
meet at 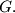 Let
Let  be the point of intersection of the lines
be the point of intersection of the lines 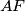 and
and  , and let
, and let  be the point of intersection of the lines
be the point of intersection of the lines 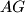 and
and 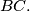 Prove that
Prove that  is the midpoint of
is the midpoint of 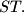
(The excircle of opposite the vertex
opposite the vertex  is the circle that is tangent to the line segment
is the circle that is tangent to the line segment  , to the ray
, to the ray  beyond
beyond  , and to the ray
, and to the ray  beyond
beyond  .)
.)
Proposed by Evangelos Psychas, Greece
 the point
the point 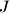 is the centre of the excircle opposite the vertex
is the centre of the excircle opposite the vertex 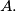 This excircle is tangent to the side
This excircle is tangent to the side  at
at  , and to the lines
, and to the lines  and
and  at
at  and
and  , respectively. The lines
, respectively. The lines 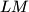 and
and 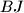 meet at
meet at  , and the lines
, and the lines 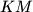 and
and 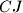 meet at
meet at 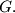 Let
Let  be the point of intersection of the lines
be the point of intersection of the lines 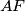 and
and  , and let
, and let  be the point of intersection of the lines
be the point of intersection of the lines 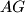 and
and 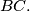 Prove that
Prove that  is the midpoint of
is the midpoint of 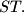
(The excircle of
 opposite the vertex
opposite the vertex  is the circle that is tangent to the line segment
is the circle that is tangent to the line segment  , to the ray
, to the ray  beyond
beyond  , and to the ray
, and to the ray  beyond
beyond  .)
.)Proposed by Evangelos Psychas, Greece
Izvor: Međunarodna matematička olimpijada, shortlist 2012
 Školjka
Školjka 
