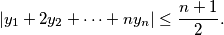In the plane the points with integer coordinates are the vertices of unit squares. The squares are coloured alternately black and white (as on a chessboard). For any pair of positive integers  and
and  , consider a right-angled triangle whose vertices have integer coordinates and whose legs, of lengths
, consider a right-angled triangle whose vertices have integer coordinates and whose legs, of lengths  and
and  , lie along edges of the squares. Let
, lie along edges of the squares. Let  be the total area of the black part of the triangle and
be the total area of the black part of the triangle and 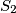 be the total area of the white part. Let
be the total area of the white part. Let 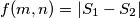 .
.
a) Calculate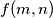 for all positive integers
for all positive integers  and
and  which are either both even or both odd.
which are either both even or both odd.
b) Prove that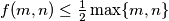 for all
for all  and
and  .
.
c) Show that there is no constant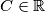 such that
such that 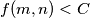 for all
for all  and
and  .
.
 and
and  , consider a right-angled triangle whose vertices have integer coordinates and whose legs, of lengths
, consider a right-angled triangle whose vertices have integer coordinates and whose legs, of lengths  and
and  , lie along edges of the squares. Let
, lie along edges of the squares. Let  be the total area of the black part of the triangle and
be the total area of the black part of the triangle and 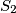 be the total area of the white part. Let
be the total area of the white part. Let 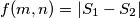 .
. a) Calculate
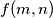 for all positive integers
for all positive integers  and
and  which are either both even or both odd.
which are either both even or both odd. b) Prove that
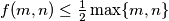 for all
for all  and
and  .
. c) Show that there is no constant
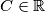 such that
such that 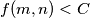 for all
for all  and
and  .
. It is known that 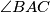 is the smallest angle in the triangle
is the smallest angle in the triangle  . The points
. The points  and
and  divide the circumcircle of the triangle into two arcs. Let
divide the circumcircle of the triangle into two arcs. Let  be an interior point of the arc between
be an interior point of the arc between  and
and  which does not contain
which does not contain  . The perpendicular bisectors of
. The perpendicular bisectors of  and
and  meet the line
meet the line 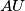 at
at  and
and  , respectively. The lines
, respectively. The lines 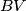 and
and 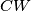 meet at
meet at  .
.
Show that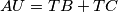 .
.
Alternative formulation:
Four different points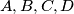 are chosen on a circle
are chosen on a circle  such that the triangle
such that the triangle  is not right-angled. Prove that:
is not right-angled. Prove that:
(a) The perpendicular bisectors of and
and  meet the line
meet the line  at certain points
at certain points  and
and 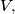 respectively, and that the lines
respectively, and that the lines 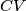 and
and 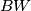 meet at a certain point
meet at a certain point 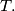
(b) The length of one of the line segments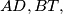 and
and 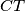 is the sum of the lengths of the other two.
is the sum of the lengths of the other two.
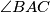 is the smallest angle in the triangle
is the smallest angle in the triangle  . The points
. The points  and
and  divide the circumcircle of the triangle into two arcs. Let
divide the circumcircle of the triangle into two arcs. Let  be an interior point of the arc between
be an interior point of the arc between  and
and  which does not contain
which does not contain  . The perpendicular bisectors of
. The perpendicular bisectors of  and
and  meet the line
meet the line 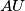 at
at  and
and  , respectively. The lines
, respectively. The lines 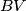 and
and 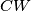 meet at
meet at  .
. Show that
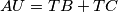 .
. Alternative formulation:
Four different points
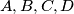 are chosen on a circle
are chosen on a circle  such that the triangle
such that the triangle  is not right-angled. Prove that:
is not right-angled. Prove that: (a) The perpendicular bisectors of
 and
and  meet the line
meet the line  at certain points
at certain points  and
and 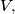 respectively, and that the lines
respectively, and that the lines 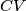 and
and 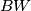 meet at a certain point
meet at a certain point 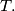
(b) The length of one of the line segments
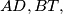 and
and 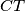 is the sum of the lengths of the other two.
is the sum of the lengths of the other two. For each positive integer  , let
, let  denote the number of ways of representing
denote the number of ways of representing  as a sum of powers of 2 with nonnegative integer exponents. Representations which differ only in the ordering of their summands are considered to be the same. For instance,
as a sum of powers of 2 with nonnegative integer exponents. Representations which differ only in the ordering of their summands are considered to be the same. For instance, 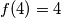 , because the number 4 can be represented in the following four ways: 4; 2+2; 2+1+1; 1+1+1+1.
, because the number 4 can be represented in the following four ways: 4; 2+2; 2+1+1; 1+1+1+1.
Prove that, for any integer we have
we have 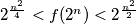 .
.
 , let
, let  denote the number of ways of representing
denote the number of ways of representing  as a sum of powers of 2 with nonnegative integer exponents. Representations which differ only in the ordering of their summands are considered to be the same. For instance,
as a sum of powers of 2 with nonnegative integer exponents. Representations which differ only in the ordering of their summands are considered to be the same. For instance, 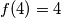 , because the number 4 can be represented in the following four ways: 4; 2+2; 2+1+1; 1+1+1+1.
, because the number 4 can be represented in the following four ways: 4; 2+2; 2+1+1; 1+1+1+1. Prove that, for any integer
 we have
we have 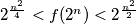 .
.  Školjka
Školjka 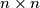 matrix whose entries come from the set
matrix whose entries come from the set 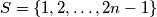 is called a silver matrix if, for each
is called a silver matrix if, for each 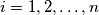 , the
, the  -th row and the
-th row and the  . Show that:
. Show that: 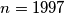 ;
; 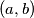 of positive integers that satisfy the equation:
of positive integers that satisfy the equation: 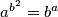 .
. 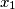 ,
, 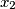 ,
,  ,
, 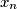 be real numbers satisfying the conditions:
be real numbers satisfying the conditions: 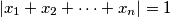 and
and 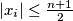 , for
, for 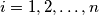
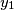 ,
, 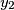 ,
, 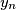 of
of