IMO Shortlist 1997 problem 1
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 In the plane the points with integer coordinates are the vertices of unit squares. The squares are coloured alternately black and white (as on a chessboard). For any pair of positive integers  and
and  , consider a right-angled triangle whose vertices have integer coordinates and whose legs, of lengths
, consider a right-angled triangle whose vertices have integer coordinates and whose legs, of lengths  and
and  , lie along edges of the squares. Let
, lie along edges of the squares. Let  be the total area of the black part of the triangle and
be the total area of the black part of the triangle and 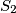 be the total area of the white part. Let
be the total area of the white part. Let 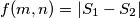 .
.
a) Calculate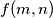 for all positive integers
for all positive integers  and
and  which are either both even or both odd.
which are either both even or both odd.
b) Prove that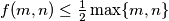 for all
for all  and
and  .
.
c) Show that there is no constant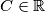 such that
such that 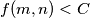 for all
for all  and
and  .
.
 and
and  , consider a right-angled triangle whose vertices have integer coordinates and whose legs, of lengths
, consider a right-angled triangle whose vertices have integer coordinates and whose legs, of lengths  and
and  , lie along edges of the squares. Let
, lie along edges of the squares. Let  be the total area of the black part of the triangle and
be the total area of the black part of the triangle and 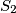 be the total area of the white part. Let
be the total area of the white part. Let 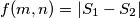 .
. a) Calculate
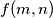 for all positive integers
for all positive integers  and
and  which are either both even or both odd.
which are either both even or both odd. b) Prove that
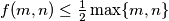 for all
for all  and
and  .
. c) Show that there is no constant
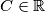 such that
such that 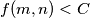 for all
for all  and
and  .
. Izvor: Međunarodna matematička olimpijada, shortlist 1997
 Školjka
Školjka 
