Konačan skup  točaka u ravnini je balansiran ako za bilo koje dvije različite točke
točaka u ravnini je balansiran ako za bilo koje dvije različite točke  i
i  u
u  postoji točka
postoji točka  u
u  takva da je
takva da je 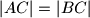 . Kažemo da je
. Kažemo da je  ekscentričan ako ni za koje tri u parovima različite točke
ekscentričan ako ni za koje tri u parovima različite točke  ,
,  i
i  u
u  ne postoji točka
ne postoji točka  u
u  takva da je
takva da je 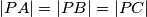 .
.
(a) Dokaži da za svaki prirodni broj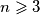 postoji balansirani skup koji se sastoji od
postoji balansirani skup koji se sastoji od  točaka.
točaka.
(b) Odredi sve prirodne brojeve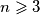 za koje postoji balansirani ekscentrični skup koji se sastoji od
za koje postoji balansirani ekscentrični skup koji se sastoji od  točaka.
točaka.
 točaka u ravnini je balansiran ako za bilo koje dvije različite točke
točaka u ravnini je balansiran ako za bilo koje dvije različite točke  i
i  u
u  postoji točka
postoji točka  u
u  takva da je
takva da je 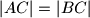 . Kažemo da je
. Kažemo da je  ekscentričan ako ni za koje tri u parovima različite točke
ekscentričan ako ni za koje tri u parovima različite točke  ,
,  i
i  u
u  ne postoji točka
ne postoji točka  u
u  takva da je
takva da je 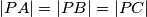 .
.(a) Dokaži da za svaki prirodni broj
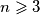 postoji balansirani skup koji se sastoji od
postoji balansirani skup koji se sastoji od  točaka.
točaka.(b) Odredi sve prirodne brojeve
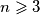 za koje postoji balansirani ekscentrični skup koji se sastoji od
za koje postoji balansirani ekscentrični skup koji se sastoji od  točaka.
točaka. Neka je  šiljastokutni trokut u kojem je
šiljastokutni trokut u kojem je 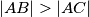 . Neka je
. Neka je  njegova opisana kružnica,
njegova opisana kružnica,  njegov ortocentar, te
njegov ortocentar, te  nožište visine iz
nožište visine iz  . Neka je
. Neka je  polovište dužine
polovište dužine  . Neka je
. Neka je  točka na kružnici
točka na kružnici  takva da je
takva da je 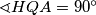 i neka je
i neka je  točka na kružnici
točka na kružnici  takva da je
takva da je 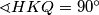 . Pretpostavlja se da su točke
. Pretpostavlja se da su točke  ,
,  ,
,  ,
,  i
i  u parovima različite i da leže na kružnici
u parovima različite i da leže na kružnici  tim redom.
tim redom.
Dokaži da su opisane kružnice trokuta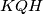 i
i 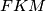 dodiruju.
dodiruju.
 šiljastokutni trokut u kojem je
šiljastokutni trokut u kojem je 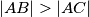 . Neka je
. Neka je  njegova opisana kružnica,
njegova opisana kružnica,  njegov ortocentar, te
njegov ortocentar, te  nožište visine iz
nožište visine iz  . Neka je
. Neka je  polovište dužine
polovište dužine  . Neka je
. Neka je  točka na kružnici
točka na kružnici  takva da je
takva da je 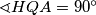 i neka je
i neka je  točka na kružnici
točka na kružnici  takva da je
takva da je 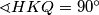 . Pretpostavlja se da su točke
. Pretpostavlja se da su točke  ,
,  ,
,  ,
,  i
i  u parovima različite i da leže na kružnici
u parovima različite i da leže na kružnici  tim redom.
tim redom.Dokaži da su opisane kružnice trokuta
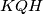 i
i 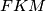 dodiruju.
dodiruju. Neka je  opisana kružnica trokuta
opisana kružnica trokuta  i
i  njeno središte. Kružnica
njeno središte. Kružnica  sa središtem
sa središtem  siječe dužinu
siječe dužinu  u točkama
u točkama  i
i  , tako da su točke
, tako da su točke  ,
,  ,
,  i
i  u parovima različite i leže na pravcu
u parovima različite i leže na pravcu  tim redom. Neka su
tim redom. Neka su  i
i  sjecišta kružnica
sjecišta kružnica  i
i  takva da točke
takva da točke  ,
,  ,
,  ,
,  i
i  leže na kružnici
leže na kružnici  tim redom. Neka je
tim redom. Neka je  drugo sjecište opisane kružnice trokuta
drugo sjecište opisane kružnice trokuta 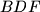 i dužine
i dužine  . Neka je
. Neka je  drugo sjecište opisane kružnice trokuta
drugo sjecište opisane kružnice trokuta 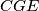 i dužine
i dužine  .
.
Pretpostavlja se da su pravci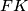 i
i 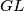 različiti i da se sijeku u točki
različiti i da se sijeku u točki  . Dokaži da točka
. Dokaži da točka  leži na pravcu
leži na pravcu 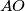 .
.
 opisana kružnica trokuta
opisana kružnica trokuta  i
i  njeno središte. Kružnica
njeno središte. Kružnica  sa središtem
sa središtem  siječe dužinu
siječe dužinu  u točkama
u točkama  i
i  , tako da su točke
, tako da su točke  ,
,  ,
,  i
i  u parovima različite i leže na pravcu
u parovima različite i leže na pravcu  tim redom. Neka su
tim redom. Neka su  i
i  sjecišta kružnica
sjecišta kružnica  i
i  takva da točke
takva da točke  ,
,  ,
,  ,
,  i
i  leže na kružnici
leže na kružnici  tim redom. Neka je
tim redom. Neka je  drugo sjecište opisane kružnice trokuta
drugo sjecište opisane kružnice trokuta 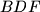 i dužine
i dužine  . Neka je
. Neka je  drugo sjecište opisane kružnice trokuta
drugo sjecište opisane kružnice trokuta 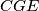 i dužine
i dužine  .
.Pretpostavlja se da su pravci
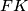 i
i 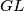 različiti i da se sijeku u točki
različiti i da se sijeku u točki  . Dokaži da točka
. Dokaži da točka  leži na pravcu
leži na pravcu 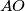 .
.  Školjka
Školjka 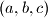 prirodnih brojeva takve da je svaki od brojeva
prirodnih brojeva takve da je svaki od brojeva 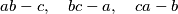 potencija broja
potencija broja  .
.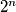 , gdje je
, gdje je 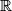 skup realnih brojeva. Odredi sve funkcije
skup realnih brojeva. Odredi sve funkcije 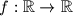 za koje vrijedi jednakosti
za koje vrijedi jednakosti 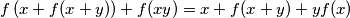 za sve realne brojeve
za sve realne brojeve  i
i  .
. 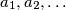 cijelih brojeva zadovoljava sljedeće uvjete:
cijelih brojeva zadovoljava sljedeće uvjete: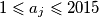 za sve
za sve 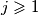 ;
;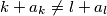 za sve
za sve 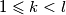 .
. i
i  takvi da je
takvi da je 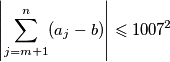 za sve cijele brojeve
za sve cijele brojeve  i
i 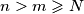 .
.