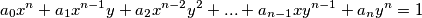Lovac i nevidljivi zec igraju igru u euklidskoj ravnini. Početna točka zeca,  , i početna točka lovca,
, i početna točka lovca, 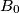 , su iste. Nakon
, su iste. Nakon  rundi igre, zec je u točki
rundi igre, zec je u točki 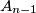 , a lovac u točki
, a lovac u točki 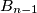 . U
. U  -toj rundi, redom se odvija sljedeće:
-toj rundi, redom se odvija sljedeće:
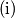 Zec se neprimjetno premješta u točku
Zec se neprimjetno premješta u točku 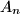 tako da je udaljenost između
tako da je udaljenost između 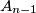 i
i 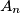 točno
točno  .
.
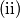 Uređaj za lociranje dojavljuje lovcu točku
Uređaj za lociranje dojavljuje lovcu točku 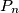 , garantirajući samo da je udaljenost itmeđu
, garantirajući samo da je udaljenost itmeđu 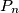 i
i 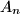 najviše
najviše  .
.
 Lovac se vidljivo premješta u točku
Lovac se vidljivo premješta u točku 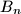 tako da je udaljenost između
tako da je udaljenost između 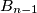 i
i 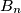 točno
točno  .
.
Može li lovac uvijek, za bilo koje pomake zeca i za bilo koje točke koje dojavi uređaj za lociranje, birati svoje poteze tako da udaljenost između njega i zeca nakon 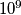 rundi bude najviše
rundi bude najviše  ?
?
Neka su  i
i  međusobno različite točke na kružnici
međusobno različite točke na kružnici  takve da
takve da 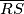 nije promjer. Neka je
nije promjer. Neka je  tangenta na kružnicu
tangenta na kružnicu  u točki
u točki  . Neka je
. Neka je  točka takva da je
točka takva da je  polovište dužine
polovište dužine 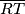 . Točka
. Točka 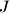 nalazi se na kraćem luku
nalazi se na kraćem luku 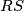 kružnice
kružnice  tako da se opisana kružnica
tako da se opisana kružnica  trokuta
trokuta 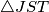 i pravac
i pravac  sijeku u dvije različite točke. Neka je
sijeku u dvije različite točke. Neka je  ono sjecište od
ono sjecište od  i
i  koje je bliže točki
koje je bliže točki  . Pravac
. Pravac 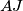 siječe kružnicu
siječe kružnicu  još u točki
još u točki  . Dokaži da pravac
. Dokaži da pravac 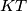 dodiruje kružnicu
dodiruje kružnicu  .
.
Dan je prirodni broj 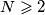 . U skupini od
. U skupini od 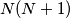 nogometaša nikoja dva nisu iste visine. Ri su nogometaši poredani u red. Trener želi iz reda izbaciti
nogometaša nikoja dva nisu iste visine. Ri su nogometaši poredani u red. Trener želi iz reda izbaciti 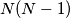 igrača tako da preostalih
igrača tako da preostalih 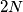 igrača tvori red za koji vrijedi sljedećih
igrača tvori red za koji vrijedi sljedećih  uvjeta:
uvjeta:
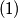 između dva najviša igrača nema nikoga,
između dva najviša igrača nema nikoga,
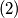 između trećeg i četvrtog igrača po visini nema nikoga,
između trećeg i četvrtog igrača po visini nema nikoga,

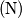 između dva najniža igrača po visini nema nikoga.
između dva najniža igrača po visini nema nikoga.
Dokaži da je to uvijek moguće napraviti.
 Školjka
Školjka 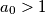 definiran je niz
definiran je niz 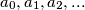 tako da je za svaki
tako da je za svaki 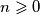

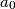 za koje postoji broj
za koje postoji broj 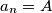 za beskonačno mnogo vrijednosti
za beskonačno mnogo vrijednosti 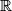 skup svih realnih brojeva. Odredi sve funkcije
skup svih realnih brojeva. Odredi sve funkcije 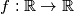 takve da za sve realne brojeve
takve da za sve realne brojeve  i
i  vrijedi
vrijedi 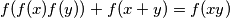
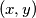 cijelih brojeva je
cijelih brojeva je 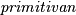 ako je najveći zajednički djelitelj brojeva
ako je najveći zajednički djelitelj brojeva 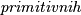 parova. Dokaži da postoje prirodan broj
parova. Dokaži da postoje prirodan broj 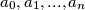 takvi da za sve parove
takvi da za sve parove 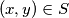 vrijedi:
vrijedi: