Let

be a positive integer and let
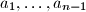
be arbitrary real numbers. Define the sequences
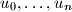
and
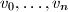
inductively by
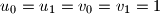
, and
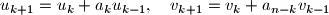
for
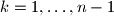
.
Prove that
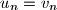
.
%V0
Let $n$ be a positive integer and let $a_1, \ldots, a_{n-1}$ be arbitrary real numbers. Define the sequences $u_0, \ldots, u_n$ and $v_0, \ldots, v_n$ inductively by $u_0 = u_1 = v_0 = v_1 = 1$, and $$
u_{k+1} = u_k + a_k u_{k-1}, \quad v_{k+1} = v_k + a_{n-k} v_{k-1}
$$ for $k = 1, \ldots, n - 1$.
Prove that $u_n = v_n$.