Trokut 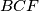 ima pravi kut u vrhu
ima pravi kut u vrhu  . Neka je
. Neka je  točka na pravcu
točka na pravcu 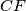 takva da je
takva da je 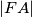 =
= 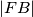 i da točka
i da točka  leži između točaka
leži između točaka  i
i  . Točka
. Točka  je izabrana tako da je
je izabrana tako da je 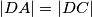 i da je pravac
i da je pravac  simetrala kuta
simetrala kuta 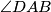 . Točka
. Točka  je izabrana tako da je
je izabrana tako da je 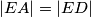 i da je pravac
i da je pravac  simetrala kuta
simetrala kuta 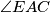 . Neka je točka
. Neka je točka  polovište dužine
polovište dužine 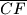 . Neka je točka
. Neka je točka  takva da je četverokut
takva da je četverokut 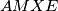 paralelogram
paralelogram 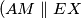 i
i 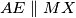 ). Dokaži da se pravci
). Dokaži da se pravci  ,
, 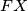 i
i 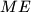 sijeku u jednoj točki.
sijeku u jednoj točki.
U ravnini se nalazi 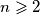 dužina takvih da se svake dvije dužine sijeku u unutrašnjoj točki i da nikoje tri dužine nemaju zajedničku točku. Geoff mora izabrati po jednu krajnju točku svake dužine i na nju postaviti žabu okrenutu prema drugoj krajnjoj točki te dužine. Potom će pljesnuti rukama
dužina takvih da se svake dvije dužine sijeku u unutrašnjoj točki i da nikoje tri dužine nemaju zajedničku točku. Geoff mora izabrati po jednu krajnju točku svake dužine i na nju postaviti žabu okrenutu prema drugoj krajnjoj točki te dužine. Potom će pljesnuti rukama  puta. Svaki put kada pljesne, svaka žaba odmah skoči prema naprijed do iduće točke presjeka na svojoj dužini. Žabe nikad ne mijenjaju smjer svojih skokova. Geoffu želi postaviti žabe tako da nikoje dvije od njih niti u jednom trenutku ne zauzimaju istu točku presjeka.
puta. Svaki put kada pljesne, svaka žaba odmah skoči prema naprijed do iduće točke presjeka na svojoj dužini. Žabe nikad ne mijenjaju smjer svojih skokova. Geoffu želi postaviti žabe tako da nikoje dvije od njih niti u jednom trenutku ne zauzimaju istu točku presjeka.
 Dokaži da Geoff uvijek može ispuniti svoju želju ako je
Dokaži da Geoff uvijek može ispuniti svoju želju ako je  neparan.
neparan.
 Dokaži da Geoff nikad ne može ispuniti svoju želju ako je
Dokaži da Geoff nikad ne može ispuniti svoju želju ako je  paran.
paran.
 Školjka
Školjka  ispuniti jednim od slova
ispuniti jednim od slova 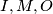 tako da su ispunjeni sljedeći uvjeti:
tako da su ispunjeni sljedeći uvjeti:
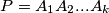 tetivan konveksni mnogokut u ravnini. Vrhovi
tetivan konveksni mnogokut u ravnini. Vrhovi 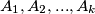 imaju cjelobrojne koordinate. Neka je
imaju cjelobrojne koordinate. Neka je  površina mnogokuta
površina mnogokuta  . Dan je neparni prirodan broj
. Dan je neparni prirodan broj 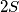 prirodni broj djeljiv sa
prirodni broj djeljiv sa 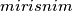 ako ima barem dva elementa i ako svaki njegov element ima barem jedan zajednički prosti djelitelj s barem jednim od preostalih elemenata. Neka je
ako ima barem dva elementa i ako svaki njegov element ima barem jedan zajednički prosti djelitelj s barem jednim od preostalih elemenata. Neka je 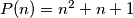 . Koja je najmanje moguća vrijednost prirodnog broja
. Koja je najmanje moguća vrijednost prirodnog broja  takva da postoji nenegativni cijeli broj
takva da postoji nenegativni cijeli broj  za koji je skup
za koji je skup 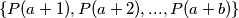
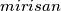 ?
? 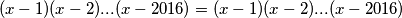
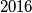 linearnih faktora. Koja je najmanja moguće vrijednost broja
linearnih faktora. Koja je najmanja moguće vrijednost broja  za koji je moguće izbrisati točno
za koji je moguće izbrisati točno 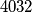 linearna faktora tako da sa svake strane ostane bar po jedan faktor i da dobivena jednadžba nema realnih rješenja?
linearna faktora tako da sa svake strane ostane bar po jedan faktor i da dobivena jednadžba nema realnih rješenja?