IMO Shortlist 1959 problem 2
Dodao/la:
arhiva2. travnja 2012. For what real values of
is
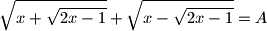
given
a)
;
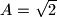
b)
;
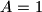
c)
,
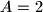
where only non-negative real numbers are admitted for square roots?
%V0
For what real values of $x$ is $$\sqrt{x+\sqrt{2x-1}}+\sqrt{x-\sqrt{2x-1}}=A$$ given
a) $A=\sqrt{2}$;
b) $A=1$;
c) $A=2$,
where only non-negative real numbers are admitted for square roots?
Izvor: Međunarodna matematička olimpijada, shortlist 1959
Školjka 
