IMO Shortlist 1959 problem 5
Kvaliteta:
Avg: 3,0Težina:
Avg: 6,0 An arbitrary point  is selected in the interior of the segment
is selected in the interior of the segment  . The square
. The square 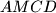 and
and 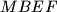 are constructed on the same side of
are constructed on the same side of  , with segments
, with segments 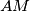 and
and 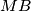 as their respective bases. The circles circumscribed about these squares, with centers
as their respective bases. The circles circumscribed about these squares, with centers  and
and  , intersect at
, intersect at  and also at another point
and also at another point  . Let
. Let 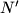 denote the point of intersection of the straight lines
denote the point of intersection of the straight lines 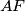 and
and  .
.
a) Prove that and
and 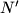 coincide;
coincide;
b) Prove that the straight lines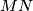 pass through a fixed point
pass through a fixed point  independent of the choice of
independent of the choice of  ;
;
c) Find the locus of the midpoints of the segments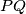 as
as  varies between
varies between  and
and  .
.
 is selected in the interior of the segment
is selected in the interior of the segment  . The square
. The square 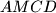 and
and 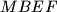 are constructed on the same side of
are constructed on the same side of  , with segments
, with segments 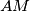 and
and 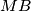 as their respective bases. The circles circumscribed about these squares, with centers
as their respective bases. The circles circumscribed about these squares, with centers  and
and  , intersect at
, intersect at  and also at another point
and also at another point  . Let
. Let 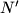 denote the point of intersection of the straight lines
denote the point of intersection of the straight lines 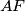 and
and  .
. a) Prove that
 and
and 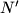 coincide;
coincide; b) Prove that the straight lines
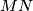 pass through a fixed point
pass through a fixed point  independent of the choice of
independent of the choice of  ;
; c) Find the locus of the midpoints of the segments
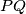 as
as  varies between
varies between  and
and  .
. Izvor: Međunarodna matematička olimpijada, shortlist 1959
 Školjka
Školjka 
