IMO Shortlist 1959 problem 6
Dodao/la:
arhiva2. travnja 2012. Two planes,

and

, intersect along the line

. The point

is given in the plane

, and the point

in the plane

; neither of these points lies on the straight line

. Construct an isosceles trapezoid

(with
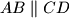
) in which a circle can be inscribed, and with vertices

and

lying in planes

and

respectively.
%V0
Two planes, $P$ and $Q$, intersect along the line $p$. The point $A$ is given in the plane $P$, and the point $C$ in the plane $Q$; neither of these points lies on the straight line $p$. Construct an isosceles trapezoid $ABCD$ (with $AB \parallel CD$) in which a circle can be inscribed, and with vertices $B$ and $D$ lying in planes $P$ and $Q$ respectively.
Izvor: Međunarodna matematička olimpijada, shortlist 1959