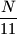
Determine all three-digit numbers having the property that is divisible by 11, and is equal to the sum of the squares of the digits of .
%V0
Determine all three-digit numbers $N$ having the property that $N$ is divisible by 11, and $\dfrac{N}{11}$ is equal to the sum of the squares of the digits of $N$.
Izvor: Međunarodna matematička olimpijada, shortlist 1960
Školjka 
having the property that 
is equal to the sum of the squares of the digits of