IMO Shortlist 1960 problem 6
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Consider a cone of revolution with an inscribed sphere tangent to the base of the cone. A cylinder is circumscribed about this sphere so that one of its bases lies in the base of the cone. let 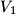 be the volume of the cone and
be the volume of the cone and 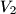 be the volume of the cylinder.
be the volume of the cylinder.
a) Prove that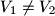 ;
;
b) Find the smallest number for which
for which 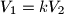 ; for this case, construct the angle subtended by a diamter of the base of the cone at the vertex of the cone.
; for this case, construct the angle subtended by a diamter of the base of the cone at the vertex of the cone.
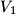 be the volume of the cone and
be the volume of the cone and 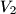 be the volume of the cylinder.
be the volume of the cylinder. a) Prove that
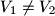 ;
; b) Find the smallest number
 for which
for which 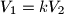 ; for this case, construct the angle subtended by a diamter of the base of the cone at the vertex of the cone.
; for this case, construct the angle subtended by a diamter of the base of the cone at the vertex of the cone. Izvor: Međunarodna matematička olimpijada, shortlist 1960
 Školjka
Školjka 
