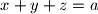
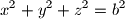
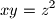
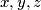
Solve the system of equations: where and are constants. Give the conditions that and must satisfy so that are distinct positive numbers.
%V0
Solve the system of equations: $$x+y+z=a$$ $$x^2+y^2+z^2=b^2$$ $$xy=z^2$$ where $a$ and $b$ are constants. Give the conditions that $a$ and $b$ must satisfy so that $x,y,z$ are distinct positive numbers.
Izvor: Međunarodna matematička olimpijada, shortlist 1961
Školjka 
where 
and 
are constants. Give the conditions that 
are distinct positive numbers.