IMO Shortlist 1961 problem 2
Dodao/la:
arhiva2. travnja 2012. Let

,

,

be the sides of a triangle, and

its area. Prove:
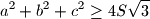
In what case does equality hold?
%V0
Let $a$, $b$, $c$ be the sides of a triangle, and $S$ its area. Prove:
$$a^{2} + b^{2} + c^{2}\geq 4S \sqrt {3}$$
In what case does equality hold?
Izvor: Međunarodna matematička olimpijada, shortlist 1961