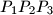
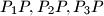
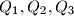
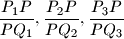
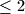
Consider triangle and a point within the triangle. Lines intersect the opposite sides in points respectively. Prove that, of the numbers at least one is and at least one is
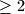
%V0
Consider triangle $P_1P_2P_3$ and a point $p$ within the triangle. Lines $P_1P, P_2P, P_3P$ intersect the opposite sides in points $Q_1, Q_2, Q_3$ respectively. Prove that, of the numbers $$\dfrac{P_1P}{PQ_1}, \dfrac{P_2P}{PQ_2}, \dfrac{P_3P}{PQ_3}$$
at least one is $\leq 2$ and at least one is $\geq 2$
Izvor: Međunarodna matematička olimpijada, shortlist 1961
Školjka 
and a point 
within the triangle. Lines 
intersect the opposite sides in points 
respectively. Prove that, of the numbers 
and at least one is 