Consider an isosceles triangle. let be the radius of its circumscribed circle and be the radius of its inscribed circle. Prove that the distance between the centers of these two circle is
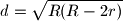
%V0
Consider an isosceles triangle. let $R$ be the radius of its circumscribed circle and $r$ be the radius of its inscribed circle. Prove that the distance $d$ between the centers of these two circle is $$d=\sqrt{R(R-2r)}$$
Izvor: Međunarodna matematička olimpijada, shortlist 1962
Školjka 
be the radius of its circumscribed circle and 
be the radius of its inscribed circle. Prove that the distance 
between the centers of these two circle is 