IMO Shortlist 1962 problem 7
Dodao/la:
arhiva2. travnja 2012. The tetrahedron
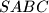
has the following property: there exist five spheres, each tangent to the edges
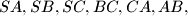
or to their extensions.
a) Prove that the tetrahedron
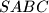
is regular.
b) Prove conversely that for every regular tetrahedron five such spheres exist.
%V0
The tetrahedron $SABC$ has the following property: there exist five spheres, each tangent to the edges $SA, SB, SC, BC, CA, AB,$ or to their extensions.
a) Prove that the tetrahedron $SABC$ is regular.
b) Prove conversely that for every regular tetrahedron five such spheres exist.
Izvor: Međunarodna matematička olimpijada, shortlist 1962