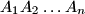
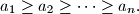
In an -gon , all of whose interior angles are equal, the lengths of consecutive sides satisfy the relation Prove that .
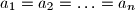
%V0
In an $n$-gon $A_{1}A_{2}\ldots A_{n}$, all of whose interior angles are equal, the lengths of consecutive sides satisfy the relation
$$a_{1}\geq a_{2}\geq \dots \geq a_{n}.$$
Prove that $a_{1}=a_{2}= \ldots= a_{n}$.
Izvor: Međunarodna matematička olimpijada, shortlist 1963
Školjka 
-gon 
, all of whose interior angles are equal, the lengths of consecutive sides satisfy the relation 
.