IMO Shortlist 1964 problem 5
Dodao/la:
arhiva2. travnja 2012. In tetrahedron

, vertex

is connected with
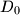
, the centrod if

. Line parallel to
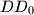
are drawn through
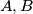
and

. These lines intersect the planes
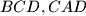
and
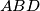
in points
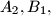
and

, respectively. Prove that the volume of

is one third the volume of
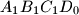
. Is the result if point
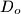
is selected anywhere within

?
%V0
In tetrahedron $ABCD$, vertex $D$ is connected with $D_0$, the centrod if $\triangle ABC$. Line parallel to $DD_0$ are drawn through $A,B$ and $C$. These lines intersect the planes $BCD, CAD$ and $ABD$ in points $A_2, B_1,$ and $C_1$, respectively. Prove that the volume of $ABCD$ is one third the volume of $A_1B_1C_1D_0$. Is the result if point $D_o$ is selected anywhere within $\triangle ABC$?
Izvor: Međunarodna matematička olimpijada, shortlist 1964