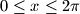
Determine all values of in the interval which satisfy the inequality
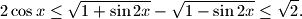
%V0
Determine all values of $x$ in the interval $0 \leq x \leq 2\pi$ which satisfy the inequality $$2 \cos{x} \leq \sqrt{1+\sin{2x}}-\sqrt{1-\sin{2x}} \leq \sqrt{2}.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1965
Školjka 
in the interval 
which satisfy the inequality 