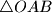
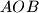
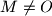
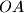
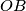
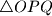
Consider with acute angle . Thorugh a point perpendiculars are drawn to and , the feet of which are and respectively. The point of intersection of the altitudes of is . What is the locus of if is permitted to range over
a) the side ;
b) the interior of .
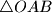
%V0
Consider $\triangle OAB$ with acute angle $AOB$. Thorugh a point $M \neq O$ perpendiculars are drawn to $OA$ and $OB$, the feet of which are $P$ and $Q$ respectively. The point of intersection of the altitudes of $\triangle OPQ$ is $H$. What is the locus of $H$ if $M$ is permitted to range over
a) the side $AB$;
b) the interior of $\triangle OAB$.
Izvor: Međunarodna matematička olimpijada, shortlist 1965
Školjka 
with acute angle 
. Thorugh a point 
perpendiculars are drawn to 
and 
, the feet of which are 
and 
respectively. The point of intersection of the altitudes of 
is 
. What is the locus of 
is permitted to range over 
;