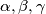
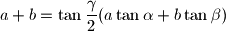
Let be the lengths of the sides of a triangle, and respectively, the angles opposite these sides. Prove that if the triangle is isosceles.
%V0
Let $a,b,c$ be the lengths of the sides of a triangle, and $\alpha, \beta, \gamma$ respectively, the angles opposite these sides. Prove that if $$a+b=\tan{\frac{\gamma}{2}}(a\tan{\alpha}+b\tan{\beta})$$ the triangle is isosceles.
Izvor: Međunarodna matematička olimpijada, shortlist 1966
Školjka 
be the lengths of the sides of a triangle, and 
respectively, the angles opposite these sides. Prove that if 
the triangle is isosceles.